東京大学先端科学技術研究センター
都築研究室
多粒子系コアダイナミクス研究室
Satori Tsuzuki's Lab.
Laboratory for core dynamics of many-particle interacting systems
Lecturer (Senior Lecturer), Principal Investigator
Research Center for Advanced Science and Technology (RCAST) ,
The University of Tokyo
Address: 4-6-1, Komaba, Meguro-Ku, Tokyo, 153-8904, JAPAN
E-mail : contact (at) satoritsuzuki.org
都築怜理, 東京大学先端科学技術研究センター講師（専任）
〒153-8904 東京都目黒区駒場4-6-1 東京大学先端科学技術研究センター
Highlighted articles
A video of the rotation simulation with the lower resolution using 2 454 000 particles from the beginning to 0.79 s in physical time.
This paper reports a three-dimensional (3D) simulation of a rotating liquid helium-4, using a two-fluid model with spin-angular momentum conservation. Our model was derived from the particle approximation of an inviscid fluid with residual viscosity. Despite the fully classical mechanical picture, the resulting system equations were consistent with those of the conventional two-fluid model. We consider bulk liquid helium-4 to be an inviscid fluid, assuming that the viscous fluid component remains at finite temperatures. As the temperature decreased, the amount of the viscous fluid component decreased, ultimately becoming a fully inviscid fluid at absolute zero. Weak compressibility is assumed to express the volume change because some helium atoms do not render fluid owing to Bose–Einstein condensations or change states because of local thermal excitation. One can solve the governing equations for an incompressible fluid using explicit smoothed-particle hydrodynamics, simultaneously reproducing density fluctuations and describing the fluid in a many-particle system. We assume the following fluid–particle duality: a hydrodynamic interfacial tension between the inviscid and viscous components or a local interaction force between two types of fluid particles. The former can be induced in the horizontal direction when non-negligible non-uniformity of the particles occurs during forced two-dimensional rotation, and the latter is non-negligible when the former is negligible. We performed a large-scale simulation of 3D liquid helium forced to rotate horizontally using 32 graphics processing units. Compared with the low-resolution calculation using 2.4 × 106 particles, the high-resolution calculation using 19.6 × 106 particles showed spinning vortices close to those of the theoretical solution. We obtained a promising venue to establish a practical simulation method for bulk liquid helium-4.
A video of the phase and density profiles of a vortex lattice formation obtained by solving the GP equation for rotating 3D BECs
Recently, we presented a new numerical scheme for vortex lattice formation in a rotating Bose–Einstein condensate (BEC) using smoothed particle hydrodynamics (SPH) with an explicit time-integrating scheme; our SPH scheme could reproduce the vortex lattices and their formation processes in rotating quasi-two-dimensional (2D) BECs trapped in a 2D harmonic potential. In this study, we have successfully demonstrated a simulation of rotating 3D BECs trapped in a 3D harmonic potential forming 'cigar-shaped' condensates. We have found that our scheme can reproduce the following typical behaviors of rotating 3D BECs observed in the literature: (i) the characteristic shape of the lattice formed in the cross-section at the origin and its formation process, (ii) the stable existence of vortex lines along the vertical axis after reaching the steady state, (iii) a 'cookie-cutter' shape, with a similar lattice shape observed wherever we cut the condensate in a certain range in the vertical direction, (iv) the bending of vortex lines when approaching the inner edges of the condensate, and (v) the formation of vortex lattices by vortices entering from outside the condensate. Therefore, we further validated our scheme by simulating rotating 3D BECs.
A video of the phase and density profiles of a vortex lattice formation obtained by solving the GP equation for rotating 2D BECs
This study proposed a new numerical scheme for vortex lattice formation in a rotating Bose–Einstein condensate (BEC) using smoothed particle hydrodynamics (SPH) with an explicit real-time integration scheme. Specifically, the Gross–Pitaevskii equation was described as a complex representation to obtain a pair of time-dependent equations, which were then solved simultaneously following discretization based on SPH particle approximation. We adopt the fourth-order Runge–Kutta method for time evolution. We performed simulations of a rotating Bose gas trapped in a harmonic potential, showing results that qualitatively agreed with previously reported experiments and simulations. The geometric patterns of formed lattices were successfully reproduced for several cases, for example, the hexagonal lattice observed in the experiments of rotating BECs. Consequently, it was confirmed that the simulation began with the periodic oscillation of the condensate, which attenuated and maintained a stable rotation with slanted elliptical shapes; however, the surface was excited to be unstable and generated ripples, which grew into vortices and then penetrated inside the condensate, forming a lattice. We confirmed that each branch point of the phase of wavefunctions corresponds to each vortex. These results demonstrate our approach at a certain degree of accuracy. In conclusion, we successfully developed a new SPH scheme for the simulations of vortex lattice formation in rotating BECs.
Schematic of the two-fluid model with angular momentum conservation
Our recent study suggested that a fully classical mechanical approximation of the two-fluid model of superfluid helium-4 based on smoothed-particle hydrodynamics (SPH) is equivalent to solving a many-body quantum mechanical equation under specific conditions. This study further verifies the existence of this equivalence. First, we derived the SPH form of the motion equation for the superfluid component of the two-fluid model, i.e., the motion equation driven by the chemical potential gradient obtained using the Gibbs–Duhem equation. We then derived the SPH form of the motion equation for condensates based on the Gross–Pitaevskii theory, i.e., the motion equation driven by the chemical potential gradient obtained from the Schrödinger equation of interacting bosons. Following this, we compared the two discretized equations. Consequently, we discovered that a condition maintaining zero internal energy for each fluid particle ensures the equivalence of the equations when the quantum pressure is negligible. Moreover, their equivalence holds even when the quantum pressure is non-negligible if the quantum pressure gradient force equals the mutual friction force. A zero internal energy indicates the thermodynamic ground state, which includes an elementary excitation state. Therefore, the condition can be sufficiently satisfied when the velocities of fluid particles do not exceed the Landau critical velocity, which is not a stringent condition for simulations with a characteristic velocity of a few cm·s−1cm·s−1 in a laboratory system. Based on the above, we performed a simulation of rotating liquid helium-4 and succeeded in generating a vortex lattice with quantized circulation, known as a quantum lattice.
(a) Schematic diagram showing the geometric correspondence between the characteristic particle arrangement observed in the SPH simulation, and (b) the Cauchy–Goursat theorem in the complex function theory.
Our recent study has shown that the representative phenomena of liquid helium-4 rotating in a cylinder could be simulated by solving the two-fluid model using smoothed-particle hydrodynamics (SPH) after reformulating the viscosity to conserve the rotational angular momentum. Specifically, the emergence of multiple parallel vortices and their rigid-body rotations were observed in our previous SPH simulations. The reported scheme is based on a classical approximation that assumes the fluid forces of both components and their interactions, with the expectation of functioning as a coarse-grained model of existing approximations that couple a microscopic model and the Navier–Stokes equation. Based on previous studies, this paper proposes an improved SPH scheme that explicitly incorporates vortex dynamics into SPH to reproduce vortex lattices, which was not possible in previous studies. Consequently, our improved scheme was observed to reproduce vortex lattices by introducing the Magnus force and interaction forces among vortices into the reformulated two-fluid model. The spinning of the vortices and rigid-body rotations were also observed. The number of vortices showed a certain agreement with Feynman's rule after the model parameter was optimized. Notably, from a scientific point of view, such vortex lattices are reproduced by the classical-mechanical approximation. We hope that our model will help physicists studying low-temperature physics find a new way of approaching this bizarre phenomenon that has attracted attention for more than 80 years.
Numerical simulation of rotating liquid 4He by solving the classical two-fluid model using smoothed particle hydrodynamics
This paper presents a finite particle approximation of the two-fluid model for liquid 4He using smoothed particle hydrodynamics (SPH). In recent years, several studies have combined the vortex filament model (VFM), which describes quantized vortices in superfluid components, with the Navier–Stokes equations, which describe the motion of normal fluids. These studies led us to assume that coupling both components of the two-fluid model instead of using the VFM to describe the superfluid component enables us to approximate the system. In this study, we formulated a new SPH model that simultaneously solves both equations of motion of the two-fluid model. We then performed a numerical simulation of the rotating liquid 4He using our SPH. The results showed that the two major phenomena, the emergence of multiple independent vortices parallel to the circular axis and that of the so-called rigid-body rotation, can be reproduced by solving the two-fluid model using SPH. This finding is interesting because it was previously assumed that only a single vortex emerges when addressing similar problems without considering quantum mechanics. Our further analysis found that the emergence of multiple independent vortices can be realized by reformulating the viscosity term of the two-fluid model to conserve the angular momentum of the particles around their axes. Consequently, our model succeeded in reproducing the phenomena observed in quantum cases, even though we solve the phenomenological governing equations of liquid 4He.
More selected articles
Delays in nerve transmission are an important topic in the field of neuroscience. Spike signals fired or received by the dendrites of a neuron travel from the axon to a presynaptic cell. The spike signal then triggers a chemical reaction at the synapse, wherein a presynaptic cell transfers neurotransmitters to the postsynaptic cell, regenerates electrical signals via a chemical reaction through ion channels, and transmits them to neighboring neurons. In the context of describing the complex physiological reaction process as a stochastic process, this study aimed to show that the distribution of the maximum time interval of spike signals follows extreme-order statistics. By considering the statistical variance in the time constant of the leaky Integrate-and-Fire model, a deterministic time evolution model for spike signals, we enabled randomness in the time interval of the spike signals. When the time constant follows an exponential distribution function, the time interval of the spike signal also follows an exponential distribution. In this case, our theory and simulations confirmed that the histogram of the maximum time interval follows the Gumbel distribution, one of the three forms of extreme-value statistics. We further confirmed that the histogram of the maximum time interval followed a Fréchet distribution when the time interval of the spike signal followed a Pareto distribution. These findings confirm that nerve transmission delay can be described using extreme value statistics and can therefore be used as a new indicator of transmission delay.
Schematic representation of a systematic description of a single neuron
Schematic of the target system; Each layer in the horizontal direction represents all possible choices in decision-making by an identical agent
This study elucidates the effect of congestion avoidance of agents given congestion information on optimizing traffic in a star topology in which the central node is connected to isolated secondary nodes with different preferences. Each agent at the central node stochastically selects a secondary node by referring to the declining preferences based on the congestion rate of the secondary nodes. We investigated two scenarios: (1) repeated visits and (2) a single visit for each node. For (1), we found that multivariate statistics describe well the nonlinear dependence of agent distribution on the number of secondaries, demonstrating the existence of the number of secondaries that makes the distribution the most uniform. For (2), we discovered that congestion avoidance linearizes the travel time for all agents visiting all nodes; in contrast, the travel time increases exponentially with secondaries when not referring to congestion information. Health examination epitomizes this finding; by allowing patients to be preferentially selected for examination in vacant examination sites, we can linearize the time it takes for everyone to complete their examination. We successfully described the optimization effect of congestion avoidance on the collective dynamics of agents in star topologies.
A graph network generated from an airport roadmap using our method
This paper proposes a method for auto-generating centerline graphs from geometrically complex roadmaps of real-world traffic systems for cellular automata simulations, using hierarchical quadtrees. Our method is summarized as follows: First, we store the binary values of the monochrome image of the target roadmap (where one and zero represent the road and other areas, respectively) in a two-dimensional square map. Second, we recursively divide the square map into sub-leaves using a quadtree, until the sum of the values of pixels included inside each leaf becomes less than or equal to one. Third, we successively remove the distal leaves for which adjacent leaves have shallower depths. Fourth, we trace the remaining distal leaves of the tree using Morton’s space-filling curve, while selecting the leaves among those selected previously that preserve a certain distance as the nodes of the graph. Finally, each selected node searches the neighboring nodes, and these are stored as the edges of the graph. We demonstrate our method by generating a centerline graph from a complex roadmap of a real-world airport, and by performing a typical network analysis using Dijkstra’s method.
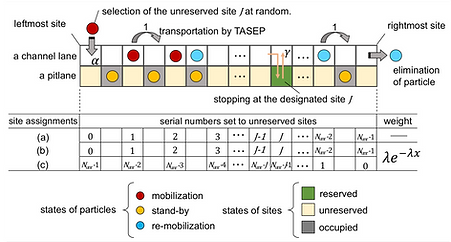
A totally asymmetric simple exclusion (TASEP) system with a queueing system along one traveling lane and a site assignment function along one parking lane
This paper proposes a totally asymmetric simple exclusion process on a traveling lane, which is equipped with a queueing system and functions of site assignments along the parking lane. In the proposed system, new particles arrive at the rear of the queue existing at the leftmost site of the system. A particle at the head of the queue selects one of the empty sites in the parking lane and reserves it for stopping at once during its travel. The arriving time and staying time in the parking sites follow half-normal distributions. The random selections of empty sites are controlled by the bias of the exponential function. Our simulation results show the unique shape of site usage distributions. In addition, the number of reserved sites is found to increase with an S-shape curve as the bias to the rightmost site increases. To describe this phenomena, we propose an approximation model, which is derived from the birth-death process and extreme order statistics. A queueing model that takes the effect of distance from the leftmost site of the traveling lane into consideration is further proposed. Our approximation model properly describes the distributions of site usage, and the proposed queueing model shows good agreement with the simulation results.
